What are the advantages of Regular Space Partitioning (RSP) over Binary Store Partitioning (BSP)?

Regular Space Partitioning (RSP) is a data structure fundamental and unique to Deephaven, and is used by all table operations. Deephaven's RSP uses, in part, the Roaring Bitmaps open source library as a building block (roaringbitmap.RoaringArray).

RSP replaces Binary Space Partitioning (BSP), the index structure used in earlier versions of Deephaven. To see the advantages of RSP in the Deephaven system, we'll first outline how BSP and RSP both work.

Binary Space Partitioning (BSP)

BSP allows the system to accumulate a set of values (i.e., an index) in a sorted array. For example, the following sorted array of only a few values is very simple and efficient:

[ 1, 5, 9, 15, 16, 19, 25 ]

To keep the array sorted when operations such as insert are performed, the system first needs to find where to put the new value. This requires a binary search on the array - O(log n). Next, space needs to be made for the new value (e.g., 10 will go after 9). Making this space does not use much memory if the set of values is small. As the set of values grows, the array is split in two around the middle (the binary space partition) and the two pieces are arranged in a tree structure.

For big indices - often accumulating millions of values - the overhead on BSP operations can be high. As a single BSP index is created and/or grows, what value moves to the top, or in other words, where the actual splitting for the "binary subdivision" happens, depends on the particular values of the index and how it was created. Operations involving mixing two indices (e.g., union, intersect, or set difference) can be very expensive because these operations need to look at the individual values on each index and decide what will happen in the result. Essentially, those operations have two iterators working in parallel, to iterate over the values of each index.

Going back to the previous example, in BSP, if we need to insert the value 10 into the array, Deephaven asks, "is the resulting array too big"? If yes, the system splits the array at a median value, creating two sub-arrays and a parent node in a tree, such as the following:

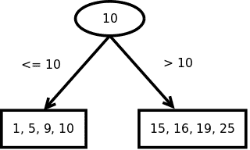
In this case, 10 is in the parent node that directs which sub-branch to descend when a search is performed.

Regular Space Partitioning (RSP)

Unlike BSP, RSP forces a partitioning at specific fixed points: it divides the space in fixed ranges of 2^16 (= 65536) values. In this data structure, an index is an array of containers, each containing at most 2^16 elements. In our BSP example, the median value 10 bubbles up in the tree to separate the two nodes (that become leaves in the tree) with the elements split between them. In RSP, this would be n*2^16 for some value of n. The key difference is that in BSP, whatever happened to be the value in the middle of the array is the point where the partitioning takes place, which bubbles up as an inner tree node. In RSP, this cannot be an arbitrary value; it must be n*2^16 for some n.

When operations such as union, set difference or intersect are performed, the system can work on the corresponding containers without caring about boundaries across containers. For instance, the position for index key 65537 can only be in the container associated with the offset 65536 (n * 2^16 with n = 1). Deephaven always knows exactly where to look when searching for an individual key.

For large datasets, RSP is usually much faster at these operations. If the system can work in pieces at a time for each operation, and guarantee that the pieces on each index align in terms of values, they can be worked on more efficiently, without having to worry about iterators crossing individual array boundaries at different points for each index.

RSP also compactly represents values. It would be inefficient to write out every single value in a big range - let's say all the values in [ 0, 10_000 * 2^16 ] - because Deephaven would have to create 10,000 containers, with all keys in each of them present. In Deephaven, we have a compact way to represent continuous ranges of values that span full blocks in [ n*2^16, m*2^16 - 1 ] space, for some value of n and m with m > n.

Nevertheless, small indices are more expensive in RSP because they are still comprised of a two-level object structure, an array of containers first, and then the containers themselves. For a small index with just a few values like [ 10, 11, 12 ], you end up with an array of one element and a container of three elements. This matters for queries that need to create one index per row (e.g., joins). The issue is alleviated by creating a special case for single-range indices (like 10-12) called SingleRangeTreeIndexImpl.