Perform fully customizable rolling aggregations

Deephaven's version 0.33 release introduced several new features and improvements. Two methods that have the potential to save users a lot of time are the new Rolling Formula update_by operations: rolling_formula_tick and rolling_formula_time. These operations support user-defined formulas, which can be used to calculate rolling aggregations over a specified window of rows or time.

Support for user-defined formulas opens up a whole new world of versatility for update_by.

This is exciting for a few reasons.

First of all, support for user-defined formulas opens up a whole new world of versatility for update_by. Rather than being limited to a single update_by operation, such as a simple Rolling Sum, users can define a custom operation that is as complex as their use cases require.

Second, Rolling Formula operations perform significantly better than calling a Rolling Group operation followed by update, which is how a user would have created a custom rolling aggregation in Deephaven version 0.32 and earlier.

rolling_formula_tick vs rolling_group_tick and update

Let's put the new rolling_formula_tick operation to the test and see just how much faster it is than the old method. In the following example, we will create a table that will run a test a given number of times, time the runs, throw out the fastest and slowest result, and print the average for each test. We will then run the test with various table sizes and unique values.

# Run tests
from deephaven.updateby import rolling_group_tick, rolling_formula_tick, rolling_sum_tick
from deephaven import empty_table
from time import time

n_rows = 1_000_000
n_unique_vals = 10_000
n_tests = 5
times_group_update = [0] * n_tests
times_formula = [0] * n_tests
times_sum = [0] * n_tests

for test_num in range(n_tests):
  test_table = empty_table(n_rows).update(f"IntCol = randomInt(0, {n_unique_vals})")

  # `rolling_group_tick` + `update` test
  start = time()
  t_grouped_updated = test_table.update_by(ops=rolling_group_tick(cols="X = IntCol", rev_ticks=1000), by=None).update("X = sum(X)")
  end = time()
  times_group_update[test_num] = end - start

  # `rolling_formula_tick` test
  start = time()
  t_formula = test_table.update_by(ops=rolling_formula_tick(formula="sum(each)", formula_param="each", cols="X = IntCol", rev_ticks=1000), by=None)
  end = time()
  times_formula[test_num] = end - start

# Print output
times_group_update.sort()
times_group_update = times_group_update[1:-1]
times_formula.sort()
times_formula = times_formula[1:-1]

print("Rolling Group + Update")
print(f"\tMin: {min(times_group_update):.4f} seconds.")
print(f"\tMax: {max(times_group_update):.4f} seconds.")
print(f"\tAvg: {(sum(times_group_update) / len(times_group_update)):.4f} seconds.")

print("Rolling Formula")
print(f"\tMin: {min(times_formula):.4f} seconds.")
print(f"\tMax: {max(times_formula):.4f} seconds.")
print(f"\tAvg: {(sum(times_formula) / len(times_formula)):.4f} seconds.")

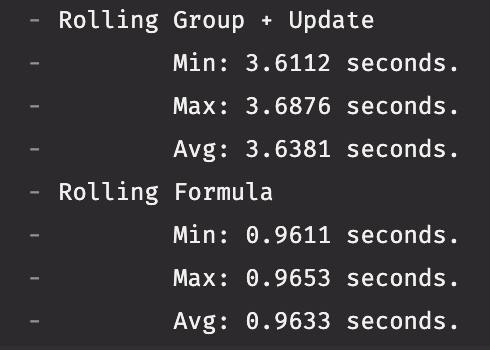
rolling_formula_tick was consistently much faster than rolling_group_tick followed by update - nearly four times faster.

This is because with rolling_formula_tick, data in the window is loaded and available for quick access by the provided formula. However, with both rolling_group_tick and rolling_formula_tick, the formula is applied to every value in the window for every ouput row, which means the performance is 0(m*n), where m is the average size of the window and n is the number of output rows.

Rolling Formula vs dedicated aggregations

Rolling Formula operations are a significant improvement over Rolling Group operations followed by update. However, Rolling Formula operations still aren't the fastest way to perform the operation in the previous example. When a dedicated aggregation exists, it's fastest to use the dedicated aggregation - in this case, rolling_sum_tick. The code block is the same as shown above, except we replace our previous test lines with a test of rolling_sum_tick.

To view the entire example in one code block, click here.

# Run tests
from deephaven.updateby import rolling_group_tick, rolling_formula_tick, rolling_sum_tick
from deephaven import empty_table
from time import time

n_rows = 1_000_000
n_unique_vals = 10_000
n_tests = 5
times_group_update = [0] * n_tests
times_formula = [0] * n_tests
times_sum = [0] * n_tests

for test_num in range(n_tests):
  test_table = empty_table(n_rows).update(f"IntCol = randomInt(0, {n_unique_vals})")

  # `rolling_sum_tick` test
  start = time()
  t_sum = test_table.update_by(ops=rolling_sum_tick(cols="X = IntCol", rev_ticks=1000), by=None)
  end = time()
  times_sum[test_num] = end - start

# Print output
times_sum.sort()
times_sum = times_sum[1:-1]

print("Rolling Sum")
print(f"\tMin: {min(times_sum):.4f} seconds.")
print(f"\tMax: {max(times_sum):.4f} seconds.")
print(f"\tAvg: {(sum(times_sum) / len(times_sum)):.4f} seconds.")

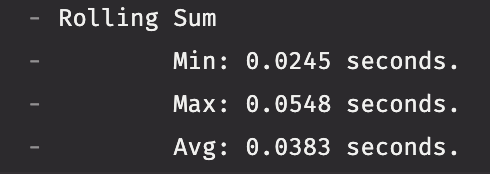
That's 25x faster than rolling_formula_tick!

Dedicated aggregations are optimized to perform the given operation as efficiently as possible and should be used whenever possible. If there is no dedicated aggregation that meets your needs, Rolling Formula operations are the next best option.

Reach out

Our Community documentation has all of the resources you need to become a Deephaven power user. Our Slack community continues to grow, and we'd love to have you join us! If you have any questions, comments, or suggestions, please reach out to us there.